đź“– Introduction to structural estimation

đź“– Introduction to structural estimation#

⏱ | words

References

Definition

Structural estimation refers to econometric methods that estimate parameters of economic models derived from economic theory, often involving optimization behavior by agents.

Historical overview#

Stage 1: Early Foundations (1930s–1950s)#

Hurwicz, Marschak, Haavelmo, Koopmans, Cowles Commission

Key contributions:

  • Introduced structural vs reduced form distinction.

  • Formalized simultaneous equations, endogeneity, identification.

  • Haavelmo (1944): probability approach to econometrics → modern estimation foundations.

  • Marschak: structure needed for policy analysis.

  • Hurwicz: identification theory (order/rank conditions).

Legacy: SEM becomes the dominant approach to causal inference in economics.

Stage 2: The Lucas Critique and Microfoundations (1970s)#

Robert Lucas and the Rational Expectations revolution

Key points:

  • Structural parameters must be policy invariant.

  • Ad hoc SEM (with “behavioral equations”) fail under policy changes.

  • Led to microfounded models derived from optimization and equilibrium conditions.

  • Birth of DSGE models as dynamic, expectations-driven SEM descendants.

Legacy: SEM concepts survive but become embedded inside microfounded dynamic systems.

Stage 3: Individual-Level Structural Modelling (1980s–1990s)#

Rust (1987): Dynamic discrete choice Hotz–Miller (1993): CCP inversion, reduced-form based identification Berry–Levinsohn–Pakes (1995): Random-coefficients demand estimation

Key innovations:

  • Microfoundations at the agent level (Bellman equations).

  • Structural estimation using NFXP and GMM.

  • Discrete choice demand becomes the IO workhorse.

Legacy: Structural microeconometrics becomes a major field.

Stage 4: Modern Structural IO (1990s–2020s)#

Ericson–Pakes (1995) \(\rightarrow\) dynamic games Aguirregabiria–Mira, Pakes et al., and more recent computational IO

Advances:

  • Multi-agent dynamic games, heterogeneous firms, entry/exit, investment.

  • GMM, simulation, and high-dimensional methods.

  • Close integration with industrial organization and antitrust practice.

Legacy: Modern IO is a fully microfounded, dynamic descendant of SEM.

From Classical SEM to Modern Structural Econometrics

          +----------------------+
          |  Classical SEM       |
          |  (Haavelmo–Marschak) |
          +-----------+----------+
                      |
                      | Microfoundations + Dynamics
                      v
          +----------------------+
          |   DSGE Models        |
          | (Dynamic SEM with    |
          |  expectations & shocks)
          +-----------+----------+
                      |
                      | Structural decision-making
                      v
          +-----------------------+
          | Dynamic Discrete      |
          | Choice Models (Rust)  |
          | Bellman eqns = system |
          +-----------+-----------+
                      |
                      | Strategic interaction + heterogeneity
                      v
          +-----------------------+
          | Structural IO         |
          | (BLP, Ericson–Pakes)  |
          | Demand + Supply as    |
          | equilibrium systems   |
          +-----------------------+

Modern structural econometric models—DSGE, dynamic discrete choice, and structural IO—are dynamic, microfounded generalizations of classical simultaneous equations models (SEM).

Structural & reduced form econometrics#

Aspect

Structural Econometrics

Reduced Form Econometrics

Definition

Estimation of parameters of economic models derived from theory

Estimation of relationships directly from the data

Purpose

Policy analysis, counterfactuals, understanding theoretical mechanisms

Prediction, local causal inference

Model

Based on economic theory, optimization behavior

Statistical relationships without explicit economic model

Assumptions

About details of economic behavior

About statistical properties of data

Identification

Exclusion restrictions, instruments, functional form

Often relies on natural experiments, IV, regression discontinuity

Estimation Methods

MLE, GMM, simulated methods

OLS, IV, matching, regression discontinuity

Data Requirements

Often requires detailed microdata

Generally less detailed or aggregate data

Applications

Structural models of demand, dynamic programming, games

Reduced form impact evaluations, treatment effects

  • Structural econometrics focuses on estimating parameters of economic models derived from theory, allowing for counterfactual analysis and policy simulations.

  • Reduced form econometrics focuses on estimating relationships directly from data without explicit reference to underlying economic models, often used for prediction or causal inference without structural interpretation.

Definition

Structural modeling is disciplined abstraction for counterfactual analysis.

Questions for discussion/reflection:

  • How can a complicated new and unique policy be evaluated without a model?

  • Should not model parameters be determined by the population under consideration?

  • Can a model be useful without being realistic? Are lab rats realistic representation of humans?

  • What does “realism” mean? Not accepting perceived conventionality?

  • Should not research challenge the conventionality by definition?

Why Structural Econometrics?#

Internal Consistency#

  • Rational agents facing constraints

  • Explicit uncertainty as probability distribution

  • Well-defined equilibrium concepts (competative, Nash, etc)

  • Explicit data-generating processes

  • Estimation grounded in LLN and CLT

Elegance and Transparency#

  • Steps can be independently verified

  • Limited discretion (though numerical implementation still may be subject to issues)

Causality#

  • A model-based concept of causality

  • Clear and explicit assumptions

Counterfactuals#

  • Generated by the model

  • Valid only within the maintained structure

  • Require external validity assumptions

Components of structural estimation project#

  1. Economic model derived from economic theory

  • Microfoundations: optimizing agents (consumers, firms)

  • With bounded rationality and behavioral extensions

  • Potentially dynamic decision-making: intertemporal choices

  • Equilibrium conditions or partial equilibrium keeping certain things fixed

  • Heterogeneity of agents: observed and unobserved differences

  • Strategic interactions (games) or infinitely small agents (aggregate market states)

  1. Data generated/described by the economic model

  • Cross-sectional, time series, or panel data

  • Individual-level or aggregate-level observations

  • Potentially censored, truncated, or missing data

  1. Preliminary data analysis

  • Data cleaning and preparation

  • Descriptive statistics

  • Visualization

  • Reduced form estimation to reduce dimensionality

  • Feed back into the economic model development

  1. Estimation method to recover structural parameters

  • Maximum likelihood (full information or limited information)

  • Generalized method of moments (GMM)

  • Simulated methods (e.g., simulated maximum likelihood, method of simulated moments)

  • Bayesian methods

  1. Identification strategy

  • Exclusion restrictions: variables that affect some equations but not others

  • Functional form assumptions: parametric or semi-parametric structures

  • Instruments for endogenous variables (BLP)

  • Policy invariance assumptions

  1. Counterfactual simulations

  • Use estimated structural parameters to simulate outcomes under different policies or scenarios

  • Estimated model is a synthetic laboratory, simulated world for policy analysis

  • Evaluate welfare effects, market outcomes, or behavioral responses

  • Conduct policy analysis based on the structural model

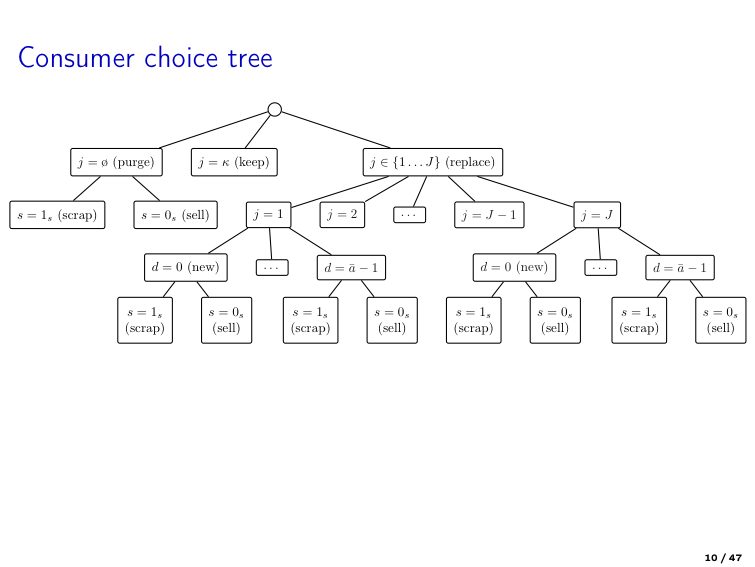
Prototype Dynamic Discrete Choice Model#

Choices#

  • Periods: \(t = 1, \dots, T\), possibly \(T = \infty\)

  • Actions: \(j = 1, \dots, J\)

  • Indicators: \(d_{jt} \in \{0,1\}\)

\[ \sum_{j=1}^J d_{jt} = 1, \; \forall t \]

Mutual exclusivity is not restrictive: combinations can be redefined as distinct actions.

States and Transitions#

Let the state be \(z_t \in \mathcal{Z}\). This is all the information that is relevant for the decision at time \(t\).

Transition probabilities when action \(j\) is chosen at period \(t\)

\[ f_{jt}(z_{t+1} \mid z_t) \]

State spaces may be large but are often sparse.

Preferences and Expected Utility#

Flow/current/instantaneous utility at time period \(t\) when action \(j\) is chosen

\[ u_{jt}(z_t) \]

Discount factor

\[ \beta \in (0,1) \]

Expected utility

\[ E\left\{\left. \sum_{t=1}^T \sum_{j=1}^J \beta^{t-1} d_{jt} u_{jt}(z_t) \right | z_1 \right\} \]

Value Functions and Bellman Equation#

Define the optimal policy \(d_t^\star(z_t)\) as vector of zeros and one indicating the most desirable action.

Value function = conditioning on optimal behavior in all future periods = maximal attainable expected utility from period

\[ V_t(z_t) = E\left\{\left. \sum_{\tau=t}^T \sum_{j=1}^J \beta^{\tau-t} d_{j\tau}^\star(z_\tau) u_{j\tau}(z_\tau) \right| z_t \right\} \]

Bellman equation:

\[ V_t(z_t) = \sum_{j=1}^J d_{jt}^\star \left[ u_{jt}(z_t) + \beta \sum_{z'} V_{t+1}(z') f_{jt}(z' \mid z_t) \right] \]

We will later see how Bellman equation can be solved and value functions computed numerically

Define choice-specific value:

\[ v_{jt}(z_t) = u_{jt}(z_t) + \beta \sum_{z'} V_{t+1}(z') f_{jt}(z' \mid z_t) \]

By definition the optimal choice is:

\[ d_{jt}^\star(z_t) = \mathbf{1} \left\{ v_{jt}(z_t) \ge v_{kt}(z_t)\, \;\forall k \right\} \]

Why Unobserved Heterogeneity Is Needed#

If agents with identical observed states are observed in the data to choose differently

  • The model implies indifference between actions

  • All actions appear optimal

  • The model loses empirical content!

Therefore fully observed heterogeneity is useless for data analysis.

Unobserved Heterogeneity Framework#

Decompose the state:

\[ z_t = (x_t, e_t) \]

  • \(x_t\): observed by both agents and econometrician

  • \(e_t\): unobserved by econometrician, but observed by agents

The objective becomes predicting choice probabilities, not individual choices.

Data Generating Process#

Observed data are states and corresponding choices:

\[ (x_1, d_1, \dots, x_T, d_T), \]

with the individual observations given by

\[ (x_1^{(n)}, d_1^{(n)}, \dots, x_T^{(n)}, d_T^{(n)}), \; n = 1, \dots, N \]

Likelihood integrates out unobservables:

\[ \Pr(d_1, x_2, \dots, d_T \mid x_1) = \int \cdots \int \prod_t \sum_{j=1}^J d_{jt} \Pr(d_t \mid x_t, e_t) \Pr(x_{t+1} \mid x_t, d_t) \, de_1 \cdots de_T \]

  • Huge multidimensional integral in general case!

  • We will see how Rust assumptions simplify this drastically

Maximum Likelihood Estimation#

Let \(\theta\) index utilities, transitions, and \(\beta\).

\[ \hat{\theta}_{ML} = \arg\max_\theta \frac{1}{N} \sum_{n=1}^N \log \Pr(\text{data}_n \mid x_{1n}; \theta) \]

Early applications include Miller (1984) and Wolpin (1984).

Other estimation approaches:

  • Two-step methods based on conditional choice probabilities estimated directly from the data (CCP methods) (Hotz–Miller, Aguirregabiria–Mira)

  • GMM

  • Method of simulated moments (MSM)

  • Calibration (no standard errors)

Multiple decision makers \(\rightarrow\) equilibrium models#

Macro style models with aggregate states#

  • Infinitely many agents

  • Individual actions do not affect aggregate states

  • Aggregate states affect individual payoffs and transitions

  • Aggregate states evolve according collective behavior of all of the agents

Dynamic Markov Games#

  • Finite number of agents

  • Individual actions affect payoffs and transitions of all other agents

  • Joint individual actions affect payoffs and transitions

  • Equilibrium defined by mutual best responses

    • Nash

    • Bayesian Nash

    • Markov Perfect Equilibrium (MPE)

    • Oblivious equilibrium, etc.

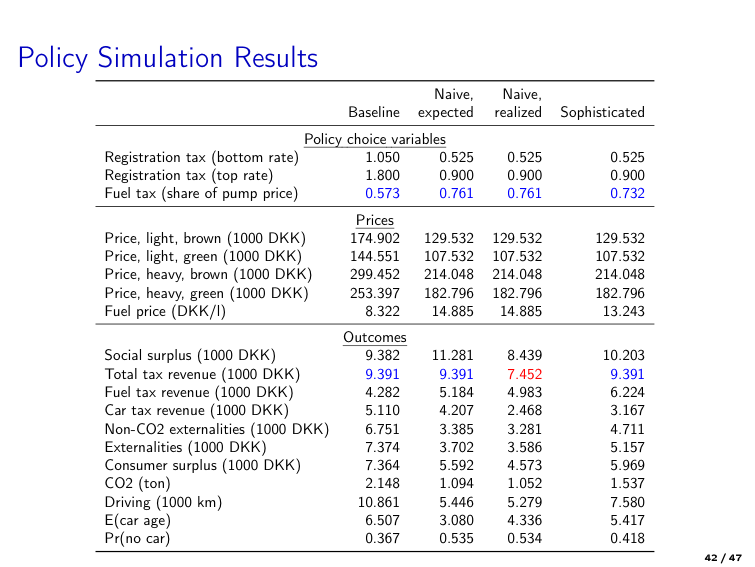
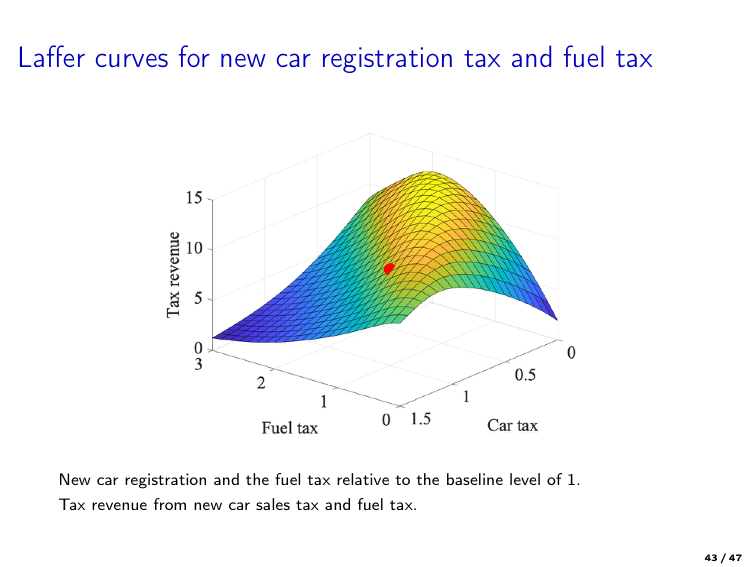
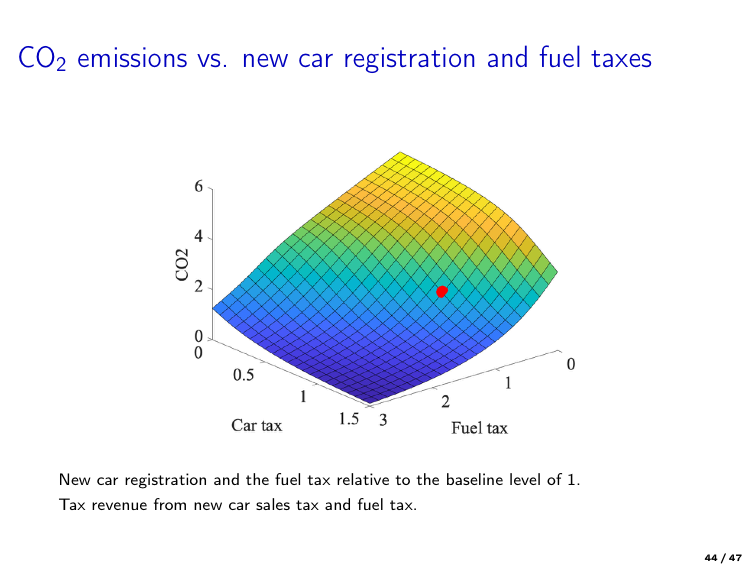
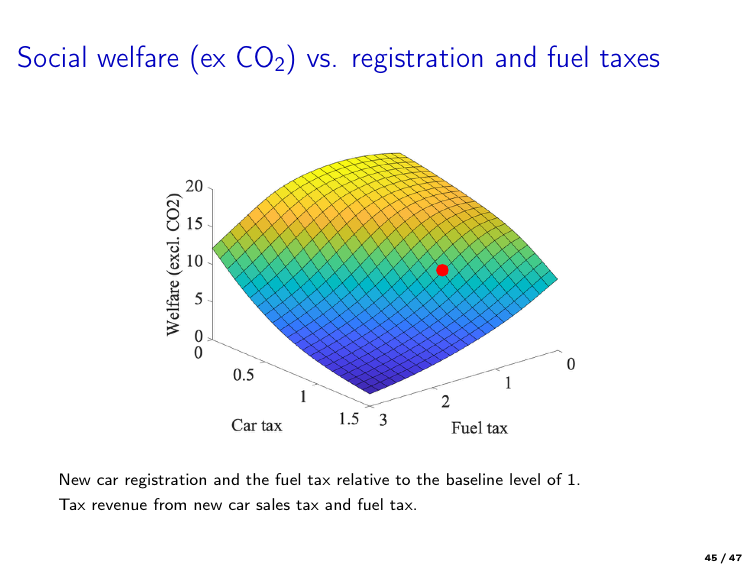
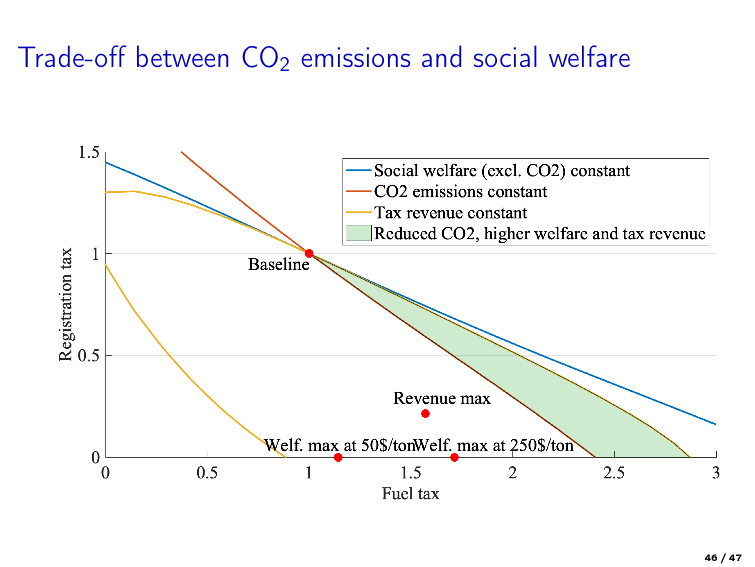
Example of policy analysis based on structural estimation

Gillingham et al. [2022] “Equilibrium Trade in Automobiles,” Journal of Political Economy

  • Policy: restructuring of car registration and fuel taxes in Denmark

  • Structural model: dynamic discrete choice model of car ownership and usage

  • Equilibrium: used car prices adjust to balance supply and demand in the secondary market

  • Estimation: MLE using Danish register data on car ownership and usage

_images/eqb_ESAM1.png _images/eqb_ESAM10.png _images/eqb_ESAM26.png _images/eqb_ESAM42.png _images/eqb_ESAM43.png _images/eqb_ESAM44.png _images/eqb_ESAM45.png _images/eqb_ESAM46.png _images/eqb_ESAM47.png

Download complete slide deck

References and Additional Resources

  • đź“– “Economic Theory and Measurement: A Twenty Year Research Report, 1932–1952” report by Cowles Commission, University of Chicago, 1952
    Download pdf

  • đź“– Keane [2010] “Structural vs. atheoretic approaches to econometrics”, Journal of Econometrics

  • đź“– Wolpin [2013] “The Limits of Inference without Theory”, The MIT Press

  • đź“– Rust [2014] “The Limits of Inference Theory: A Review of Wolpin (2013)”, Journal of Economic Literature

  • đź“– Sargent [2024] “Critique and consequence”, Journal of Monetary Economics 2024

  • Michael Keane’s lecture on structural estimation at BFI at the University of Chicago https://youtu.be/0hazaPBAYWE

Contents